簡而言之，零點是分析反饋系統穩定性的一種方式。

我會盡量避免過於沉重的數學運算，但是我不確定如何在不加說明的情況下進行解釋至少是一些數學。

這是反饋系統的基本結構：

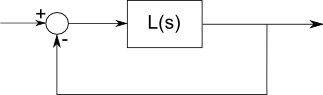
在這種形式下，反饋中沒有增益或補償路徑，它完全放在前向路徑中，但是，可以將更通用的系統的反饋部分轉換為類似形式並以相同的方式進行分析。

框中的傳遞函數稱為\ $ L（s）\ $，因為分析通常是在Laplace變換空間中完成的。拉普拉斯變換類似於傅立葉變換，因此您可以將L（s）視為頻率響應。例如，一個完美的低通濾波器的\ $ L（s）= 1 \ $小於截止頻率\ $ s \ $，而\ $ L（s）= 0 \ $高於截止頻率。

\ $ L（0）\ $是系統的直流增益。對於反饋控制系統，理想的是大的DC增益，因為它會減小系統的穩態跟踪誤差。

極點和零點

\ $ L（s）\ $是複數值函數。通常使用極性形式\ $ A e ^ {i \ theta} \ $； $ A $是幅值，\ $ \ theta \ $是相位。 \ $ L（s）\ $的大小也稱為增益。

極點和零點提供了一種方便，快捷的方式來考慮\ $ L（s）\ $的屬性。當繪製\ $ L（s）\ $的粗略圖時，極點在極點頻率之上貢獻了-90°的相位，並導致幅度“下降”（減小）。零則相反—它們貢獻+ 90°的相位，並且幅度增加。通過查看圖片和 http://en.wikipedia.org/wiki/Bode_plot的“手工製作波特圖的規則”部分，這可能會更有意義。

要使系統穩定，在相位達到-180°之前（以較低的頻率），\ $ L（s）\ $的大小必須降到1以下。通常，這裡需要一些保證金； “增益裕度”和“相位裕度”是兩種測量\ $ L（s）\ $與（1，-180°）點的距離的方法。

作為一個簡單的示例，運算符-amp可能具有\ $ L（s）= \ frac {10 ^ {6}} {s} \ $。在這種情況下，極點為零，沒有零。正如您對運算放大器的期望一樣，直流增益很大。增益隨頻率從DC增加而下降（由於極點為零）。根據此模型，系統不會不穩定，因為相位永遠不會小於-90°。

在閱讀有關極點和零點的應用筆記時，您可能需要弄清楚相位的一般形式\ $ L（s）\ $用於所討論的系統，或者您可以僅從極點和零點列表中得出一些結論。給系統增加一個極點或零點都會改變增益和相位裕度。將極點和零點加在一起（在不同頻率下，都在-180°交叉點以下）將改變增益裕度，但不會改變相位裕度。相加兩個零和兩個極點可以在\ $ L（s）\ $（認為帶通濾波器）中產生一個駝峰，而不會改變增益或相位裕度。

希望這會有所幫助。通常，我希望數據表和應用筆記會為補償組件提供建議值，這樣，除非有特殊要求，否則用戶無需分析穩定性。如果您想使用某個特定的部分時遇到麻煩，並在數據表中發布了鏈接，我也許可以提供一些幫助。

1. 可以使用複雜函數\ $ L（s）\ $描述反饋系統（如任何其他AC電路）。它稱為系統的傳遞函數，描述了系統的所有線性行為。

2. \ $ L（s）\ $可以繪製為兩個圖：一個表示幅度，另一個表示一個用於相位與頻率的關係（Body圖）。這些圖使我們可以輕鬆確定係統的穩定性。不穩定的系統會獲得180°的相移（因此負反饋突然開始為正），同時仍具有一定的增益。

3. 每個描述電路的複函數都是完全由極點和零點定義如果將函數寫為\ $ j \ omega \ $的兩個多項式的比率，則零是分子等於\ $ 0 \ $的點，極點是分母的零。

4. 從極點和零點繪製波特圖非常容易，因此它們是指定控制系統的首選方法。同樣，如果您可以忽略輸出負載（因為使用運算放大器將各個級分開），則只需乘以傳遞函數即可，而無需進行所有常規電路計算。多項式比率的乘積意味著您可以串聯極點和零點的列表。

ol>

所以回到您的問題：

1. 在 Wikipedia頁面中獲得介紹，並在本教程中獲得有關如何從極點和零點列表繪製Bode圖的參考。

2. 閱讀一些有關 Laplace變換中的實用內容的信息。簡短的版本：您只需要用複數來計算電路，但是用\ $ s \ $代替要寫\ $ j \ omega \ $的位置。然後您找到\ $ V_ {out} \ over V_ {in} \ $，您就擁有了轉移功能。

3. 從開環傳遞函數（想像用剪刀剪開環並在其中放入某種頻率響應計），您可以繪製波特圖並驗證穩定性。 反饋，運算放大器和補償應用筆記簡短而密集，但具有該部分所需的全部理論。嘗試至少瀏覽一下。

ol>

一個簡單的隔直電容器，例如用於耦合音頻放大器的電容器，其原點為零-隔斷0Hz信號，即隔斷恆定電壓。

通常，我們關於復雜的頻率。我們不僅考慮像傅立葉所做的那樣是正弦/餘弦波之和的信號；我們提出關於正弦/餘弦呈指數增長或衰減的理論。表示此類信號的極點和零點可以位於復平面中的任何位置。

如果一個極點靠近實軸，代表正常的穩定正弦波，則代表一個調諧良好的帶通濾波器，就像高質量的LC電路一樣。如果距離較遠，那是一個糊狀的軟帶通濾波器，具有較低的“ Q”值。相同的直觀推理也適用於零-零接近實軸時，響應譜中的切口更清晰。

描述濾波器響應的傳遞函數L（s）的極點數和零點數應相等。這是複雜分析中的一個基本事實，這是正確的，因為我們正在處理由簡單代數，導數和積分描述的線性集總成分，並且我們可以將正弦/餘弦描述為複雜的指數函數。這種數學無處不在。但是，通常不提及極點處的極點或零點。

這兩個實體（如果不在實軸上）將成對出現-以復數頻率及其複共軛形式出現。這涉及以下事實，即，實際信號輸入會導致實際信號輸出。我們不測量複數電壓。 （在微波世界中，事情變得越來越有趣。）

如果L（s）= 1 / s，則在原點為極點，在無窮大處為零。這是積分器的功能。施加恆定電壓，增益為無窮大-輸出無限制地上升（直到達到電源電壓或電路冒煙）。相反，將非常高的頻率置於積分器中將不會產生任何效果。隨著時間的流逝，它平均為零。

“右半平面”中的極點表示在某個頻率下的共振，該共振使信號呈指數增長。因此，您希望極點位於左半平面，這意味著對於任何放入濾波器的任意信號，輸出最終將衰減為零。那是一個普通的過濾器。當然，振盪器應該振盪。由於非線性，它們可以保持穩定的信號-晶體管輸出的電壓不能超過Vcc或小於0伏。一個極點，並且每次下降都為零，但是嚴格來說並非如此。遠離真實軸的零點和零點的影響並不明顯。如果有人發明了Flash或Java Web小程序，讓您在任何地方移動幾個零點並繪製響應，那將是很好的。

所有這些都被簡化了，但是應該給出一些關於極點和零點含義的直觀認識。

讓我嘗試將其簡化為比以前發布的詳細解釋還要簡單的術語。

首先要意識到的是，對於控制系統類型，零點和零點意味著我們是在Laplace域中。創建Laplace變換是為了允許以代數方式處理微分方程和積分方程。拉普拉斯方程式中的“ s”表示“的導數”，“ 1 / s”表示“取整數”。但是，如果您有一個傳遞函數為（1 + s）的塊，然後是另一個傳遞函數（TF）為（3-5 / s）的塊，則只需乘以（1 + s）就可以得到總傳遞函數）（3-5 / s）並得到（3s-5 / s-2），這比在常規域中處理積分和導數要容易得多。

因此，對這個問題->極點表示整個傳遞函數具有一個's'，其值無窮大。 （您可以想像，這通常是一件非常糟糕的事情。）零意味著完全相反：值s會導致總T.F。 =0。這是一個示例：

一個TF是（s + 3）/（s + 8）。這個TF在s = -3處有一個零，在s = -8處有一個極。

極是必不可少的惡魔：為了做任何有用的事情，例如使真實係統的輸出跟踪輸入，您絕對需要兩極。您經常需要設計一個以上的系統。但是，如果您不注意設計，那麼這些極點中的一個或多個極點可能會誤入“等於實數為正的數字”（即平面的右半部分）。這意味著系統不穩定。除非您有意構建振盪器，否則這通常是非常糟糕的。

大多數開環系統都具有極點和零點，這些極點和零點很容易表徵並且表現良好。但是，當您有意（或無意地，這非常容易做到）獲取一部分輸出並將其反饋給系統的某些早期部分時，便創建了一個閉環反饋系統。閉環極點和零點與開環極點和零點有關，但與休閒觀察者所不了解的方式無關。只需說這就是設計師經常遇到麻煩的地方即可。這些閉環極點需要停留在拉普拉斯平面的左側。實現此目的的兩種最常用技術是控制通過閉環路徑的整體增益和/或加零（開環零點喜歡開環極點，並且經常使閉環極點的行為大不相同）。 >

對上面得到高度評價的答案進行快速評論：“總之，零點是分析反饋系統穩定性的一種方式。”

儘管陳述是正確的，但係統卻沒有這樣做。不必徵求反饋，這些概念才有用。極點和零點對於理解大多數具有頻率響應而不是平坦響應的實際系統很有用，例如濾波器，放大器和任何類型的動態系統。

要添加一些數學運算（我們必須這樣做，這是一個數學概念），您可以（對於許多系統）將系統的頻率響應表示為：

H（f）= B（f）/ A（f）

以及B（f）和A（f）可以表示為頻率上的複多項式。

一個簡單的示例：考慮一個RC低通濾波器（電壓輸入->系列R->分流C->電壓輸出）。

可以表示增益（傳遞函數）在頻域中為：

Vout（f）/ Vin（f）= H（f）= 1 /（1 + j * 2 * pi * f * R * C），

其中j（或i）是-1的平方根。

在頻率fp = 1 /（2 pi RC）處有一個極點。如果繪製此復數方程的幅值，您會發現DC處的增益為1（0dB），在f = fp = 1 /（2 * pi * RC）時增益降至-3dB，並且增益為極點之後，頻率繼續以每十年-20dB的幅度下降（增加10倍）。這個簡單的例子是一個低通濾波器，其“角頻率”為w = 1 /（RC）或f = 1 /（2 pi RC）。

在數學上，極點是分母。類似地，零是分子的根，增益在高於零的頻率處增加。相位也會受到影響...但是對於非數學線程而言，這可能綽綽有餘。

“階”是極數，而“類型”是f = 0時的極數（純積分器）。