我將使用微控制器創建用於電機控制的PWM信號。我了解PWM和占空比的工作原理，但是我不確定理想的頻率。我還沒有電機，所以我不能僅僅進行測試並找出答案。
我不會改變電壓，只是當它收到給定電壓時。那麼我可以假設線性響應嗎？在10％的佔空比和24 V的電源下，它將以15 RPM的速度運行？
如果有所作為，我將包括設置。我直接將24 V電源連接到控制電機的H橋。顯然，我從MCU到兩個使能MOSFET的門都有兩個PWM引腳。
編輯：對不起，該鏈接似乎無效。我猜防火牆在工作中不喜歡imgur。圖片描繪了RPM與電壓的關係圖。從50 RPM @ 8 V到150 RPM @ 24 V是線性的。
簡而言之：
您可以通過施加pwm信號來線性控制'速度'，現在該信號的頻率必須足夠高，以使您的直流電動機僅通過PWM信號的直流分量，這只是平均值。將電動機視為低通濾波器。如果您查看傳遞函數或角速度與電壓之間的關係，這就是您的經驗
$$ \ frac {\ omega（s）} {V（s）} = \ frac {K} {\ tau s + 1} $$ 這是直流電動機的一階模型，或者只是截止頻率為$$ f_c = \ frac {1} {2 \ pi \ tau} $$
的低通濾波器其中\ $ \ tau \ $是電動機的時間常數。因此，只要您的頻率超過截止頻率，您的電動機將僅看到DC部分或PWM信號的平均值，並且您的速度將與PWM佔空比一致。當然，如果您的頻率很高，則應該考慮一些折衷...
L長故事：
理論上，您需要知道電動機的時間常數，才能選擇“正確的” PWM頻率。您可能知道，電機達到最終值幾乎100％所需的時間為$$ t_ {final} \約5 \ tau $$
您的PWM頻率必須足夠高，以使電動機（本質上是低通濾波器）對您的輸入電壓（即方波）求平均。例如，假設您有一台時間常數為\ $ \ tau = 10ms \ $的電動機。我將使用一階模型來模擬其對多個PWM週期的響應。這是直流電動機型號： $$ \ frac {\ omega（s）} {V（s）} = \ frac {K} {10 ^ {-3} s + 1} $$
為了簡單起見，我們讓\ $ k = 1 \ $。
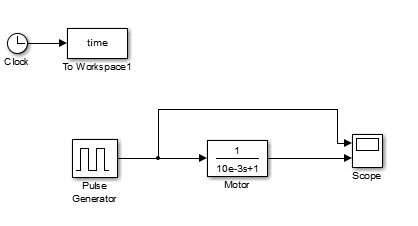
但更重要的是，這裡是我們正在尋找的答案。對於第一個示例，PWM週期為\ $ 3 \ tau \ $，佔空比為50％。這是電機的響應：
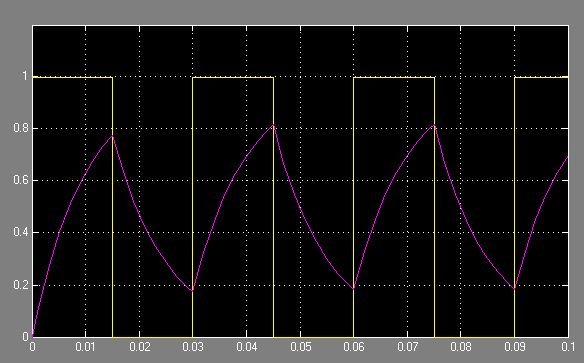
黃色圖是PWM信號（佔空比為50％，週期為\ $ 3 \ tau = 30ms \ $），紫色為電動機的速度。如您所見，由於PWM的頻率不夠高，電動機的速度會大幅波動。
現在讓我們增加PWM頻率。PWM週期現在為\ $ 0.1 \ tau = 1ms \ $，佔空比仍然為50％。
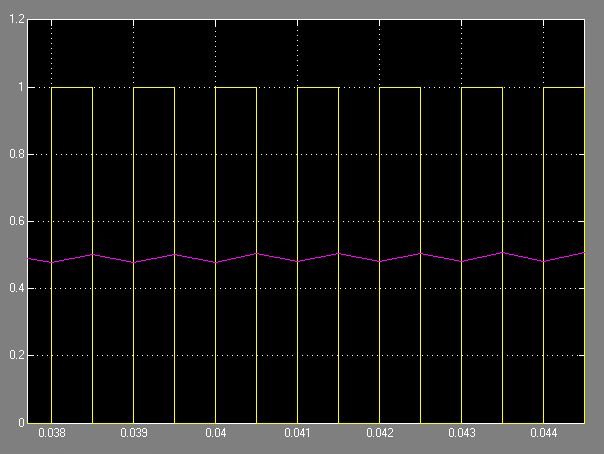
如您所見，由於pwm信號的高頻成分已被濾除，因此速度現在幾乎是恆定的。 總之，我選擇的頻率至少為\ $ f_s \ geq \ frac {5} {2 \ pi \ tau} \ $。
這只是有關如何選擇PWM頻率的非常理論性的解釋。希望對您有幫助！
您的電動機可能會減速，因為150 rpm的轉速僅為每秒2.5轉。在50 rpm的轉速下，您的電動機需要一秒鐘以上的時間才能完成一轉。
話雖如此，您的H橋中的開關在導通（基本上為零伏）或關斷（為零電流）時不會消耗太多功率。它們在切換時僅同時具有電壓和電流，因此更高的切換頻率意味著FET中的熱量更多。
保持在5-20 KHz範圍內，您可能會很安全。如果調得太低，電動機電流紋波（和轉矩紋波）可能會很明顯，但是您可以嘗試一下。太高了，您將加熱開關。您可能還想朝更高端走出可聽範圍。
實際電動機的行為大致類似於與真實電動機串聯的電阻器和電感器。為了有效運行，您需要在將電動機連接到電源與短路之間切換。當電動機連接到電源時，電流將變得更正。當做空時，它將變得更加不利。如果電流切換極性，效率將顯著下降，因為電動機將在每個週期中花費一部分時間來嘗試機械地抵抗其他部分的工作。
從電動機本身的角度來看，當PWM速率盡可能高時，效率將達到最佳。但是，有兩個因素限制了最佳PWM速率：
許多電動機都與電容器並聯，以最大程度地減少電磁干擾。每個PWM週期都需要對該電容進行充電和放電，從而浪費了全部能量。此處的損耗與頻率成正比。
許多H橋開關需要一定的時間才能切換；當它們切換時，進入它們的大部分功率將被浪費。隨著PWM的開啟和關閉持續時間縮小到電橋花費其大部分活動或不活動時間切換的點，切換損耗將增加。
最關鍵的是，PWM速率必須足夠快，以至於電動機不會自fight。更快地超過該速度將在某種程度上提高電動機效率，但以增加上述其他損失為代價。如果沒有太多的並聯電容，那麼在PWM損耗最小且電機電流極性保持正向的情況下，通常會有相當大的頻率範圍。在該範圍中間附近的某個頻率可能是最好的，但是在該範圍內的任何東西都應該足夠。
幾年前，我設計並開發了PWM速度/位置控制系統，該系統驅動了16台有刷直流電動機。我們是從Mabuchi購買的，該公司當時每年售出3.5億台電動機。他們建議使用2 kHz PWM頻率，該頻率與當時包括遙控飛機在內的其他來源的建議相吻合。我們取得了很好的結果，從那以後我就開始使用它。
有一種理論認為，高於20 kHz的頻率意味著沒有嘯叫/雜音，但我們發現事實並非如此。我不知道它的真正物理原理，但是可以聽到機械運動。我是對還是錯，都認為它是頻率的次諧波（正確的短語？），因為線圈或組件試圖在高頻下如此輕微地移動，但無法跟上。我在家中有手機充電器，可以清楚地聽到嘯叫聲，而且我知道他們的PWM振盪器在100 kHz以上的頻率下運行良好。 （事實上，我經常在走過廚房時關閉它，因為在沒有連接電話的情況下，我會聽到較高的“空載”口哨聲。當我第一次插入電話時，我還會聽到聲音逐漸降低的聲音。 ）
如果電動機和驅動器支持，有時希望保持在可聽頻率（20KhZ）以上。如果有人聽到它，那麼恆定的高音調頻率可能會令人討厭。年輕人可以聽見，到40歲以後，聲音逐漸減小。