我正在做一個簡單的實驗（我是一個愛好EE），以增強歐姆定律數學，並學到一些有關如何用萬用表進行正確測量的知識。
一個與LED串聯的2.2k歐姆電阻。一切正常，直到可以計算電阻器和LED兩端的壓降為止。
我最初的計算僅考慮了2.2k歐姆電阻器。這樣，我得到了電阻兩端的全壓降。但是，當我對電路進行實際測量時，我發現結果幾乎是輸入電壓的一半，這向我表明
唯一要說明的就是LED。確定簡單LED電阻的最佳方法是什麼？我嘗試用電阻器進行操作（用手指將其固定在探頭上），但讀數不正確。我這裡缺少一種技術嗎？
最好不要將LED建模為純電阻器。正如在其他一些答案中指出的那樣，真實的LED確實具有電阻，但是在對二極管進行建模時，通常並不是主要考慮的問題。 LED的電流/電壓關係圖：
現在，這種行為很難手動計算（特別是對於復雜的電路），但是有一個很好的“近似值”將二極管分為3種離散工作模式：
如果二極管兩端的電壓大於 Vd ，則二極管的行為就像一個恆定的電壓降（即它將允許任何電流通過以維持 V = Vd ）。
如果電壓小於 Vd 但大於擊穿電壓
Vbr 時，二極管不導通。
如果反向偏置電壓高於擊穿電壓
Vbr ，二極管再次導通，並且將允許任何電流通過以保持 V = Vbr 。
所以，讓我們假設一些電路：
模擬該電路 –使用 CircuitLab sup>
首先，我們假設t VS > Vd 。這意味著 R 兩端的電壓為 VR = VS-Vd 。
使用歐姆定律，我們可以知道流過R的電流（因此D）是：
\ begin {equation} I = \ frac {V_R} {R} \ end {equation}
讓我們插入一些數字。說 VS = 5V ，R = 2.2k ， Vd = 2V （典型的紅色LED）。
\ begin {equation} V_R = 5V -2V = 3V \\ I = \ frac {3V} {2.2k \ Omega} = 1.36 mA \ end {equation}
好，如果 VS = 1V ，R怎麼辦= 2.2k ，而 Vd = 2V ？
這次是 VS < Vd ，並且二極管不導通。沒有電流流過 R ，因此 VR = 0V 。這意味著 VD = VS = 1V （此處， VD 是 D 上的實際電壓，其中 Vd 是二極管的飽和壓降。
與其他一些答案相反，LED 確實具有電阻。它很小，但並不重要。僅僅靠電阻還不足以表徵其行為，但是說LED不具有 電阻僅是有時的有效簡化。
例如，來自 LTL-307EE的數據表中的這張圖，除了它是CircuitLab中的默認二極管和一個非常典型的指示器LED外，我無緣無故地選擇了它：
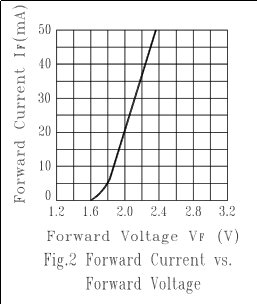
看看線在5mA以上如何基本筆直，而不垂直嗎？那是由於LED的內部電阻。這是引線，鍵合線和矽的電阻之和。
不帶電阻的LED在電流 \ $ I \之間具有指數關係。 $ span>和電壓 \ $ V_D \ $ span>，根據 Schockley二極管方程：
$$ I = I_S \ left（e ^ {V_D /（nV_T）}-1 \ right）$$ span>
我不會讓您感到厭煩所有術語的定義：如果您想了解更多信息，請閱讀Wikipedia。只知道它們對於給定的LED是常數。查看 \ $ I \ $ span>和 \ $ V_D \ $ span>術語，並查看它們之間的指數關係。在此示例中，我選擇了 \ $ V_T = 25.85 \ cdot10 ^ {-3} \ $ span>， \ $ n = 1 \ $ span>和 \ $ i_s = 10 ^ {-33} \ $ span>。
請考慮a的電流-電壓關係電阻，由歐姆定律給出：
$$ I = \ frac {V} {R} $$ span >
顯然，它們是線性相關的。如果要像上面的數據表那樣繪製電阻器的電流-電壓關係圖，您會得到一條直線，穿過 \ $ 0V，0A \ $ span>，而這條線的斜率就是電阻 \ $ R \ $ span>。
下面是帶有電阻的圖形，“理想根據肖克利二極管方程式且沒有電阻的二極管，以及更實際的包括一些電阻的LED模型：
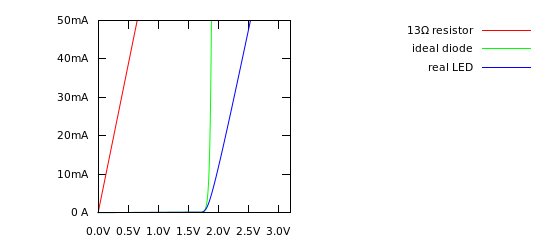
> 5 mA，理想的二極管看起來像一條垂直線。它實際上只是非常陡峭，但在此範圍內看起來是垂直的。但是真正的LED不能做到這一點，甚至不能關閉。如果您在上面的數據表中查看該線的斜率，則它看起來像是一條從（1.8 V，5 mA）到（2.4 V，50 mA）的直線。該線的斜率是：
$$ \ frac {2.4 \：\ mathrm V-1.8 \：\ mathrm V} {50 \：\ mathrm { mA} -5 \：\ mathrm {mA}} = \ frac {0.6 \：\ mathrm V} {45 \：\ mathrm {mA}} = 13 \：\ Omega $$ span>
因此，LED的內部電阻為13Ω。
當然，您還必須在計算中包括LED的正向壓降，這將導致LED的正向壓降向右移動。 電阻器和真實LED 線。但是，其他人已經做了很好的解釋。
最終，您只需要對LED的那些對您的應用至關重要的方面進行建模。如果要再增加1000Ω，則13Ω的電阻並不重要。如果LED僅打開或關閉，則電流-電壓曲線中的拐點並不重要。但是，為了理解您正在做的簡化假設，以及當這些簡化假設不再有效時，我想解釋一下：LED 確實具有抵抗力。
通常，二極管不具有電阻（除了封裝內部導體中的少量電阻），但是二極管上確實存在壓降，其壓降取決於其結構中使用的半導體材料。對於典型的LED，此電壓降為〜1.5V。電壓降與半導體中的帶隙（最高束縛電子態與“導帶”之間的能量差）有關。該電壓降確實在一定程度上取決於溫度和電流，但對於簡單的LED應用而言並沒有很大關係。達到閾值電壓。請注意，與電阻不同，IV曲線非常非線性。
如果不使用電阻將二極管直接連接到電池，則二極管中的電流僅由佈線中的電阻（很小）和電池的內部電阻決定，因此二極管中的電流會很大，並且（最有可能）會消耗掉，因為二極管本身不提供任何電阻，而是導電當前。
要回答您的問題，為了計算流過二極管的電流，您需要確定電源電壓，減去二極管壓降，然後使用這個新的較低電壓通過限流電阻器來計算電流。
LED具有內置的壓降（由於LED的特性）。您可以查看購買的LED的規格表來確定壓降。 LED的顏色通常會影響其兩端的電壓降。
更多詳細說明：
“電阻”的概念有兩個相關含義。最簡單的意思就是說，在任何時刻，兩點之間的路徑的電阻定義為這些點之間的電壓與流經該路徑的電流量之比。將該定義視為“定律”的原因是，對於由許多材料構成的路徑（尤其是當Geor Ohm提出該定義時已知的路徑），電壓與電流之比將隨著電壓和電流的變化而大致保持恆定變化。因此，如果知道在某個電壓下有多少電流流經一條路徑，則可以使用導出的量“電阻”來預測在其他電壓下有多少電流流過，或者需要多少電壓才能引起其他電流量。流動。
對於由多種材料製成的路徑，歐姆定律很好地描述了電壓與電流之間的關係，但是對於由其他材料製成的路徑，電壓與電流之比並不是恆定的。但是，即使有許多這樣的圖形，如果要繪製電壓與電流的關係圖，也會在該圖的某些區域中該直線相當筆直。當電壓和電流在這樣的區域上時，將器件建模為與理想電阻串聯的理想電壓源可能會有所幫助。假設的LED兩端的電壓在+0至+1.5範圍內時（可能幾乎沒有電流流過），其行為可能幾乎是無限電阻，而當LED兩端的電壓為1.7V時，它會與100歐姆電阻串聯。電壓大於2.0伏。在圖表上繪製這些行為會產生兩個不相交的線段，並且在它們之間留有間隙。 LED的行為將是一條連接這兩條線的曲線，儘管歐姆定律並不真正適合於嘗試預測該區域的曲線。
